Tx=20231020.

Eine Spule für den SAQ

Zum Empfang des schwachen SAQ-Signals auf 17.2 kHz soll ein Resonanzkreis ganz weit vorne zum Einsatz kommen um einerseits andere Signale früh auszufiltern (und vom Rest des Empfängers fern zu halten, sodass es zu keinen Intermodulationsprodukten kommt) und andererseits durch Resonanzüberhöhung die Empfangsspannung anzuheben. Dafür bedarf es einer Spule mit hoher Güte, damit das schwache Empfangssignal nicht gleich wieder weggedämpft wird. Hier wollen wir untersuchen, wie wir eine Spule mit hoher Induktivität (ca. 12 mH) und hoher Güte herstellen können. Einige Fragen sind: wie ist die Spule zu wickeln (langgezogen oder kurz und hoch oder Kraut und Rüben?), ist ein, zwei, drei, vier Ferritstäbe besser, oder ein Ringkern oder ein Schalenkern, kann ich fertige Drosseln aus einem Schaltnetzteil verwenden, welche Güte kann erreicht werden, muss HF-Litze verwendet werden oder reicht Kupferlackdraht, ist eine Rahmenantenne besser, ... ?

Für die Messung mit dem Oszi ist unbedingt das QM-1 abzuschalten (alle Röhrenheizungen aus!), sodass die Röhren kalt sind und einen hohen Widerstand haben, denn sie belasten sonst den Schwingkreis zu sehr (auch die vom VTVM). Diese Belastung muss wohl in die Eichung des Instruments des QM-1 bereits mit eingeflossen sein. Andererseits führt die Belastung durch die 1:10 Tastspitze des Oszi's zu keiner merklichen Änderung des Ausschlags des QM-1, sodass die Tastspitze bei allen Messungen angeschlossen bleiben kann.

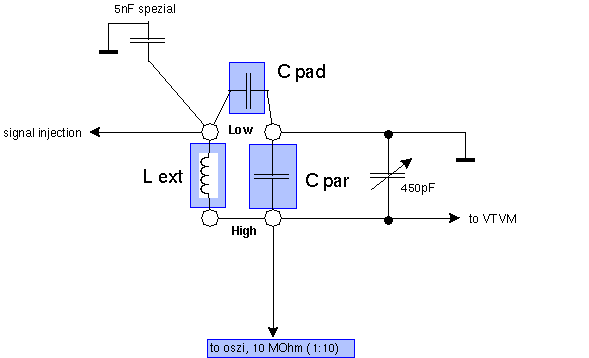
Hier die Beschaltung für den Anschluss des padding Kondensators Cpad zwischen den beiden Low-Terminals. In blau sind externe Komponenten hinterlegt.

Mit dem grossen padding Kondensator von 143nF kann das QM-1 nur noch höhere Güten messen, weil zwar Resonanz auftritt, aber bei den tiefen Frequenzen nur noch sehr wenig HF-Energie über den kleinen Koppelkondensator (ca. 10pF) eingekoppelt wird, die dann auch noch über den grossen padding Kondensator teilweise nach Masse abfliesst. Der Faktor zwischen Anzeige und Q beträgt dann 29.6, die kleinste ablesbare Güte ist ca. 5, sodass die kleinste messbare Güte bei 148 liegt, was bei den niedrigen Frequenzen kaum erreicht wird. Daher findet sich dann n/a in den Zellen, die nicht gemessen werden können.

Für die Messungen mit dem Oszi verwenden wir diese Schaltung:

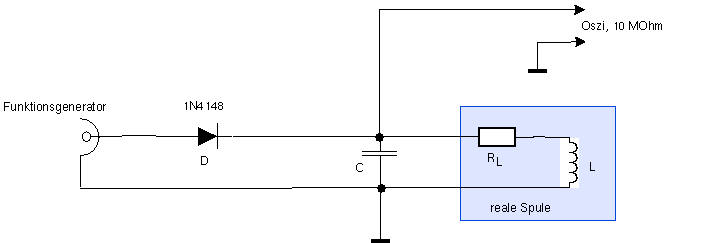
Die Diode entkoppelt Schwingkreis und Funktionsgenerator, der mit einer Rechteckschwingung niedriger Frequenz (z.B. 41 Hz damit das Bild nicht flackert) und mit einem Tastverhältnis, das dem Schwingkreis genug Zeit zum Ausschwingen gibt (also eine lange LOW Phase und nur eine kurze HIGH Phase, etwa 9:1), den Schwingkreis periodisch anregt. Während der HIGH Phase prägen wir der Spule einen gewissen Strom I ein (die absolute Größe spielt keine Rolle). Schaltet der Funktionsgenerator auf LOW, so müssen wir ihn vom Schwingkreis trennen, weil er diesen sonst viel zu stark belasten würde. Das machen wir mit der Diode D: diese sperrt (und wird hochohmig) sobald der Funktionsgenerator auf LOW schaltet (wir können am Funktionsgenerator auch noch zusätzlich einen kleinen negativen DC-Offset einstellen, um die Diode schnell und sicher sperren zu lassen). Als Drehkondensator können wir wieder das QM-1 verwenden, jedoch sollte es abgeschaltet sein (alle Röhren kalt).  Die beiden Low-Anschlussklemmen werden hier mit einem Draht direkt verbunden, sodass der padding Kondensator aus der Schaltung entfernt wird.

Wir stellen die Amplitude zu Beginn auf 4 Kästchen ein und messen die Zeit bis die Spannung auf 1.5 Kästchen abgesunken ist.

Q =  (   * ) / 2 = * f *





Eine tolle Beschreibung der Verhältnisse beim Detektorempfänger inklusive Diskussion von Güte und Spulenaufbau wurde von Kainka durhgeführt. Sehr informativ zu lesen!

Was lernen wir daraus?

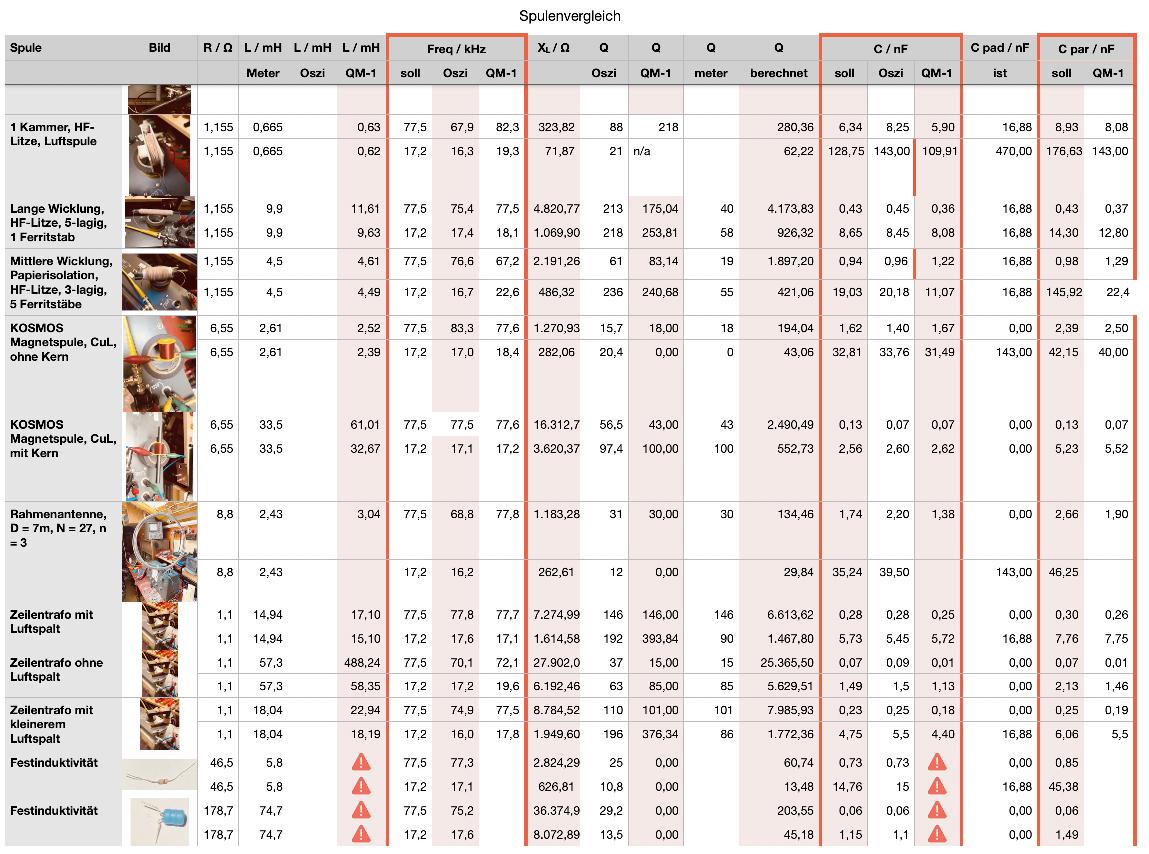
Real vs. berechnet
Es fällt auf, dass die gemessenen Q-Werte stets kleiner sind, als die berechneten. In die Berechnung geht ja nur der Ohm'sche Widerstand des Drahtes ein, jedoch gibt es noch mehr Verlusteffekte, die sich real auswirken, daher ist der effektive reelle Widerstand stets größer, was zu einer kleineren Güte führt. Das ist also verständlich und nachvollziehbar.

Q = XL / R = * L / R
XL = * L

Der Unterschied ist vor allem bei den höheren Frequenzen besonders ausgeprägt, da dort die zusätzlichen Dämpfungseffekte stärker zu Buche schlagen: die Kernverluste (sofern ein Kern vorhanden ist) steigen mit der Frequenz, ebenso der Skineffekt, der ab ca. 100 kHz als wesentlich erachtet wird. Auch das ist also verständlich. Ebenfalls wird klar, dass der Ohm'sche Widerstand von 1.1 Ohm nicht die bestimmende Größe für die Dämpfung ist, sondern dass da andere Dinge wesentlich wichtiger sind, da wir eine sehr grosse Abweichung zwischen berechneter und gemessener Güte haben (Faktor 6.5!).

Um eine optimale Spule zu finden, reicht die Berechnung also nicht, eine Messung, die auch alle parasitären "Dreckeffekte" berücksichtigt, ist erforderlich!



Frequenzabhängigkeit der Güte
Die obige Formel für die Berechnung von Q sagt klar, dass die Güte linear mit der Frequenz ansteigt, wenn alle anderen Einflüsse gleich bleiben. Dies kann durch die Messungen aber nicht bestätigt werden: überraschender Weise ist die Güte bei niedrigen Frequenzen höher (!) als bei den nur moderat höheren Frequenzen von 77kHz. Dies kommt uns natürlich zugute und liegt wohl an den höheren Kernverlusten bei den höheren Frequenzen (obwohl diese Ferritkerne eigentlich für Mittelwelle ausgelegt sind). Für die reine Luftspule gibt es diesen Effekt nicht, dort ist die Güte bei 17 kHz schlechter als bei 77 kHz. Es liegt also nicht am Skin-Effekt, der ja durch die Verwendung von HF-Litze unterdrückt werden sollte -- passt.

Mit Ferritkern ist die Güte bei 17 kHz höher als bei 77 kHz!



Kern oder Luftspule?
Vor allem bei 17 kHz müssen wir die maximale Induktivität aus der Drahtlänge herausholen, um ein höheres Q zu erhalten. Dafür ist ein Kern unerläßlich. Je länger der Kern, umso höher die Induktivität, auch wenn die Spule nur einen kleinen Bereich des Kerns überdeckt. Interessant: bei zwei Kernen ist nicht die Anordnung mit beiden Kernen in der Mitte die beste, sondern wenn sich die beiden Kerne nach beiden Seiten der Spule weit hinauserstrecken, aber nicht maximal. Ein zweiter Kern bringt keine Verdoppelung, aber eine Erhöhung. Das Kernmaterial muss für die Frequenzen natürlich ausgelegt sein und niedrige Verluste haben.

Übrigens ist das Maximum der Indusktivität nicht, wenn die Spule in der Mitte des Stabs ist, sondern wenn sie leicht einseitig verschoben ist.

Ohne Kern ist die Spulengüte durchweg schlechter als mit Kern, obwohl hier die Kernverluste wegfallen. Dies liegt vermutlich an der drastisch gesunkenen Induktivität, die zusammen mit den wesentlich grösseren Kondensatoren für wesentlich höhere Ströme im Schwingkreis sorgt, sodass sich der Ohm'sche Widerstand stärker auswirkt.

Es scheint mir, dass nicht alle Ferritstäbe gleich gut sind, sondern bei 77 kHz deutliche Unterschiede in Bezug auf Verluste haben. Man müsste untersuchen, welcher Stab gut und welcher schlecht ist. Nach meinem Kenntnisstand sind die schwarzen Ferritstäbe für Frequenzen  bis ca. 2 MHz geeignet, die grauen Stäbe für Frequenzen bis ca. 5MHz. Bei kleinen Frequenzen haben die schwarzen Stäbe eine höhere Permeabilität r.

Unbedingt einen großen (langen und dicken) Kern verwenden!



Lange oder kurze Spule?
Die Standardformel zur Berechnung der Induktivität L, N: Windungszahl, A: Querschnittsfläche, l: Spulenlänge

L = 0 * r * N2 * A / l

sagt ganz klar, dass eine kurze, "dicke" (grosses A)  Spule eine höhere Induktivität hat, als eine lange, dünne Spule. Die Messungen zeigen aber das glatte Gegenteil! Die lange Spule mit nur 5 Lagen um nur einen Ferritstab hat satte 9.9 mH während die dicke Spule mit dem gleichen Draht nur 2.72 mH zustande bringt. Ich habe das N, die Zahl der Windungen, nicht gezählt, aber klar ist, dass bei kleinerem Durchmesser (dünne Spule) die gleiche Drahtlänge für mehr Windungen reicht. Dieser Effekt kürzt sich aber heraus:

A = r2 *         ; Querschnittsfläche
U = 2 * * r     ; Umfang
D: Drahtlänge
N = D / U

L(r) = 0 * r * N2 * A / l
= 0 * r * (D / U)2 * A / l
= 0 * r * (D2 * r2 * ) / (4 * 2 * r2 * l)
= 0 * r * D2 / (4 * l

Bei gegebener, fester Drahtlänge D spielt die Querschnittsfläche also keine Rolle mehr. Eine kurze Spule wird aber immer noch bevorzugt. Warum ist das bei uns aber anders?
Ich denke, das liegt am (langgestreckten) Kern und seiner Geometrie. Der Kern bündelt ja viele Feldlinien in seinem Inneren, jedoch gehen auch viele in der anderen Richtung nahe am Kern zurück. Daher wird nur eine Spule, die wirklich nahe am Kern bleibt, von seiner Bündelung den größten Vorteil ziehen. Dadurch muss sie halt dann notgedrungen länger werden, was zwar nicht gut ist, aber durch die Nähe zum Kern mehr als kompensiert wird. Möglicherweise gibt es ein Optimum, was die Zahl der Lagen (Dicke der Spule) und ihre Länge angeht. Es ist aber aufwändig, dies experimentell zu bestimmen, da jedes Mal die Spule neu gewickelt werden müsste.

Für ein grosses L ist direkt auf den Ferritstab zu wickeln. Die Spule soll kurz sein, kann aber auch die ganze Länge überstreichen. Durch die Nähe zum Kern wird allerdings das Q wieder schlechter. Für ein besseres Q ist die Spule etwas vom Kern entfernt zu halten (und kürzer), für ein grösseres L näher am Kern (aber dann sinkt das Q).

Kurze Spule, etwas vom Kern entfernt, aber nicht zu weit weg.



HF-Litze oder CuL?
Die KOSMOS Spule mit Kern erreicht eine beachtliche Induktivität von 33.5 mH. Sie ist mit CuL gewickelt. Trotzdem erreicht sie eine Güte von 100 bei 17.2kHz. Bei 77.5 kHz sinkt die Güte aber dann auf die Hälfte, diese Abnahme war bei HF-Litze nicht so stark spürbar. Auch ist der Ohm'sche Widerstand mit 6.5 Ohm ca. 6 mal größer als bei der Spule mit HF-Litze. Die Drahtlänge oder Zahl der Windungen N ist leider nicht bekannt. Man kann festhalten, dass CuL bei den niedrigeren Frequenzen durchaus geeignet ist, insbesondere, wenn etwas dickerer Draht verwendet wird. Die Güte ist zwar nur halb so groß wie mit HF-Litze, jedoch ist CuL wesentlich billiger. Eine Güte von 100 erscheint mir ausreichend, denn zu große Güten verzögern das Ausschwingen nach einem Morsezeichen sehr, sodass das Lesen schwieriger wird ("nachklingeln"). Bei Q = 100 und f = 17.2 kHz ergibt sich eine Ausschwingzeit von ca. 2ms, was bei 60 bpm keine Probleme verursachen sollte (60 bpm = 180 Zeichen pro Minute = im Mittel 3 Zeichen pro Sekunde (ohne Pausen) = 6 Zeichen pro Sekunde mit Pausen = 160 ms pro Zeichen (Punkt oder Strich oder Pause)).

CuL kann auf 17.2 kHz mit Abstrichen verwendet werden



Rahmenantenne
Wir haben mit der Gleichung vorher schon gesehen, dass die Induktivität im Wesentlichen nur von der Drahtlänge D abhängt.

L = 0 * r * D2 / (4 * l

Es spielt also kaum eine Rolle, ob der Draht mehrfach aufgewickelt ist, oder wir nur eine grosse Windung haben -- allerdings hat dies einen Einfluss auf die Wicklungslänge l, welche möglichst klein sein sollte. Ich habe ein Stück CAT V twisted pair Kabel von 2.10 m Länge gefunden, das ich verwenden will. Die twisted pairs sind bereits geschirmt, sodass die Antenne möglichst keine elektrischen Störungen aus nächster Nähe aufnehmen sollte, sondern nur die magnetische Komponente vom Fernfeld des Senders (SAQ). Ich kann damit entweder eine Spule mit  n =1 Windung (was dann wegen der 4 twisted pairs N = 8 realen Windungen entspricht) mit 66 cm Durchmesser aufbauen, oder n = 3 Windungen (N = n * 8 = 3 * 8 = 24) und 22 cm Durchmesser. Im zweiten Fall ist l etwas größer, dafür ist die Spule handhabbarer. Die berechnete Induktivität beträgt leider nur L = 2.8 mH -- sie sollte eigentlich grösser sein. Ein Leiter hat einen Widerstand von 135 mOhm für die 2.10 m Länge. Alle 8 haben also 1.1 Ohm, was dem Wert der HF-Litze von vorher entspricht.

Ein anderes twisted pair Kabel hat ca. D = 7 m Länge, die Adern sind flexibel als Litze ausgeführt, jedoch hat eine Ader ca. 1 Ohm Widerstand, das wären dann 9 Ohm Gesamtwiderstand (es ist eine rote Bonusader enthalten), was schon recht hoch ist, aber laut berechnetem L = 39.4 mH und Q = 483 (Tabelle!) noch vertretbar ist. Ich werde dieses Kabel verwenden und n = 6 Windungen wickeln, damit die Fläche A groß wird, die Spule aber noch handhabbar bleibt. Zu meiner grossen Überraschung ist das gemessene L = 2.4 mH wesentlich kleiner! Der Grund ist, dass die übliche Formel nur gilt, wenn die Länge l der Spule deutlich grösser als ihr Durchmesser ist. Bei einer derart kleinen Induktivität ergibt sich rechnerisch nur eine sehr kleine Güte von ca. Q = 30, die reale Güte liegt mit Q = 12 nochmals darunter. Das sind keine guten Voraussetzungen, auch wenn die grosse Fläche A vermutlich den Empfang verbessert (mehr Feldlinien, Fluß).

Eine höhere Güte und Induktivität ergibt sich mit der Ferritantenne.



Zeilentrafo
Wirklich überraschend ist die hohe Induktivität des Zeilentrafos, die zusammen mit dem niedrigen Ohm'schen Widerstand zu sehr hohen Güten führt. Allerdings bemerken wir bei 77 kHz, wie erwartet, ein starkes Absinken der Güte, was wohl auf Verluste im Kernmaterial zurückzuführen ist, da dieses nur für 16 kHz ausgelegt ist. Aber immer noch beachtlich gut, der Zeilentrafo ist definitiv auch bei 77 kHz verwendbar!

Überraschend ist, dass das Entfernen des Luftspalts die Güte drastisch einbrechen lässt, sogar auf 17.2 kHz!  Das hätte ich nicht erwartet. Klar ist, dass ohne Luftspalt die Induktivität stark zunimmt, gleichzeitig steigt auch der berechnete Q-Wert extrem an. Trotzdem ist die reale Güte deutlich schlechter als mit Luftspalt! Das kann nur bedeuten, dass die Kernverluste nun dominieren, auch wenn hier keine nennenswerte Leistung umgesetzt wird.

Ich habe dann einen neuen Luftspalt mit nur 1 Plättchen von 0.2 mm Dicke in jedem Schenkel probiert (vorher waren auf einer Seite zwei Plättchen (aus dem 3D-Drucker) drin, auf der anderen Seite nur 1 Plättchen). Die Induktivität fiel ab, aber die Güte stieg deutlich an und erreichte einen Wert zwischen den beiden anderen. Zusaätzlich habe ich die Antennenspule und die Rückkopplungsspule entfernt (obwohl beide vorher nicht angeschlossen waren).

Es ist auch im Empfangskreis ein Luftspalt zu verwenden, um eine hohe Güte zu erreichen.



Festinduktivitäten
Die teilweise erheblichen Induktivitätswerte dieser kleinen Dinger haben mich sehr überrascht. Zuerst hielt ich 100 mH für einen Tippfehler (das soll wohl 100 H heissen?!), aber es stimmt! Diese kleinen Induktivitäten halten, was draufsteht! Unglaublich, wenn ich das mit der Ferritantenne oder dem Zeilentrafo oder auch alten Schalenkernen vergleiche. Aber man zahlt halt auch einen Preis: der Draht muss wohl super dünn sein, denn der Ohm'sche Widerstand ist wesentlich höher als bei allen anderen untersuchten Spulen. Entsprechend sind die berechneten Güten schon recht niedrig, die gemessenen Güten (ich habe hier nur noch mit dem Oszi gemessen) sind nochmals schlechter, aber nicht so krass, wie bei den anderen Spulen. Für einen selektiven, empfindlichen Schwingkreis sind diese Bauteile nur bedingt geeignet (vielleicht, wenn man den Schwingkreis per Rückkopplung entdämpft). Dafür sind sie super klein und man spart sich das nervige Wickeln von Spulen. Ich denke, als Drosseln (etwa in Anodenleitungen) oder bei kräftigeren Signalen weiter hinten im Empfänger könnte man sie schon verwenden.



Fazit
Ich werde Empfangsversuche mit der KOSMOS-Spule (mit Ferritstab), der Ferritantenne (1 Stab, lange Spule, HF-Litze) und der Rahmenantenne durchführen, denn Q alleine ist sicher nicht der einzige Faktor für einen guten Empfang.

Links
Gütefaktor im LC Kreis Theorie vs Praxis
Gütemessung mit Rechtecksignal
LC Resonance Calculator
Träger einige kHz neben DCF77?
Induktivität einer Spule berechnen



Zurück zur Hauptseite