Tx=20231016.

Der Q-Faktor: die Güte

Schwingkreise werden im Hochfrequenzbereich oft und gerne eingesetzt. Eine Hauptanwendung ist die Selektion einer gewünschten Station aus dem Brei aller sendenden Stationen. Dazu wird der Schwingkreis auf die Frequenz des gewünschten Senders abgestimmt und durch Resonanzüberhöhung der Spannung erscheint dann dessen Signal mit wesentlich größerer Amplitude, während alle anderen Sender abgeschwächt werden. Ein Nachteil ist, dass die Impedanz des Schwingkreises bei Resonanz sehr hoch wird (geht im Idealfall gegen unendlich), man darf den Schwinkreis also nur sehr wenig belasten (10 MOhm), um die Schwingung nicht zu stören.

Eine andere Anwendung, vor allem in Röhrenschaltungen, ist die Transformation eines Stromsignals in ein Spannungssignal. Eine Röhre liefert an ihrem Ausgang ja ein Stromsignal in Form des Anodenstroms, braucht aber am Eingang der nächsten Stufe ein Spannungssignal für das Steuergitter. Hierfür ist ein Schwingkreis sehr gut geeignet, denn die Belastung durch das nachfolgende Gitter ist sehr klein und seine hohe Impedanz ist auch für den Anodenkreis gut geeignet (die Verstärkung der Stufe steigt ja mit der Größe des Anodenwiderstands). Gleichzeitig dient die Spule als Weg für den Gleichstromanteil des Anodenstroms.

Durch Verwendung von Anzapfungen kann die Impedanz an die Ausgangsimpedanz der Röhre angepasst werden, da vor allem Trioden eine eher kleine Ausgangsimpedanz haben. Andererseits kann durch Verwendung einer Koppelwicklung zum einen eine galvanische Trennung der hohen Anodenspannung vom empfindlichen Gitter erfolgen, zum anderen kann hier ebenfalls auf die richtige Impedanz transformiert werden, um den Schwingkreis nicht zu sehr zu belasten oder um eine besonders hohe Amplitude am Gitter zu erzeugen.

Ach du meine Güte!
Um eine möglichst grosse Resonanzüberhöhung oder eine scharfe Selektivität zu bekommen, was im Allgemeinen das Ziel ist, muss der Schwingkreis möglichst frei schwingen können. Dazu ist es wichtig, dass die Dämpfung des Schwingkreises möglichst gering ist. Dies ist gleichbedeutend damit, dass einmal angeregte Schwingungen möglichst lange anhalten und nur langsam abklingen. Wie können wir das erreichen?

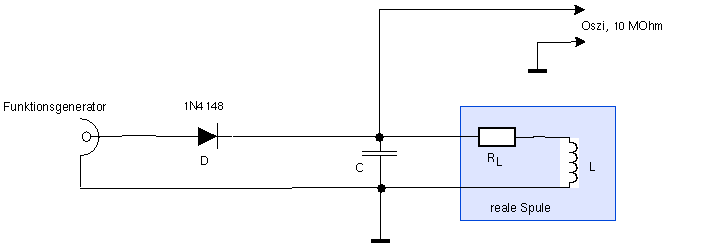
Im normalen LC-Kreis trägt vor allem die Spule durch ihren ohm'schen Widerstand (Drahtwiderstand) zur Dämpfung bei, während übliche Kondensatoren kaum Verluste haben. Im folgenden Schaltbild ist die reale Spule blau hinterlegt: sie besteht aus einer idealen Spule L (ohne Verluste und ohne Drahtwiderstand) und einem angenommenen Widerstand R_L der den Drahtwiderstand der Spule symbolisiert. Mathematisch können alle weiteren Spulenverluste, wie etwa Verluste im Eisenkern (Kernverluste), Skineffekt, Proximity-Effekt, Strahlungsverluste, etc., in diesem Widerstand R_L zusammengefasst werden. Der Widerstand R_L kann also nicht immer einfach mit dem Ohmmeter bestimmt werden, jedoch ist das sicher eine gute erste Näherung.

Am LC Parallelschwingkreis können wir direkt mit dem Oszillographen messen, jedoch nur mit der 1:10 (10 MOhm) oder 1:100 (100 MOhm) Tastspitze, denn die Eingangsimpedanz von 1 MOhm des Oszi kann schon zu Verfälschungen der Messung führen, weil sie den Schwingkreis zu sehr belastet.

Die Anregung machen wir am besten mit dem Funktionsgenerator mit einer Rechteckschwingung niedriger Frequenz (z.B. 41 Hz damit das Bild nicht flackert) und mit einem Tastverhältnis, das dem Schwingkreis genug Zeit zum Ausschwingen gibt (also eine lange LOW Phase und nur eine kurze HIGH Phase, etwa 9:1). Während der HIGH Phase prägen wir der Spule einen gewissen Strom I ein (die absolute Größe spielt keine Rolle). Schaltet der Funktionsgenerator auf LOW, so müssen wir ihn vom Schwingkreis trennen, weil er diesen sonst viel zu stark belasten würde. Das machen wir mit der Diode D: diese sperrt (und wird hochohmig) sobald der Funktionsgenerator auf LOW schaltet (wir können am Funktionsgenerator auch noch zusätzlich einen kleinen negativen DC-Offset einstellen, um die Diode schnell und sicher sperren zu lassen).

Das Oszillogramm sieht dann so aus:

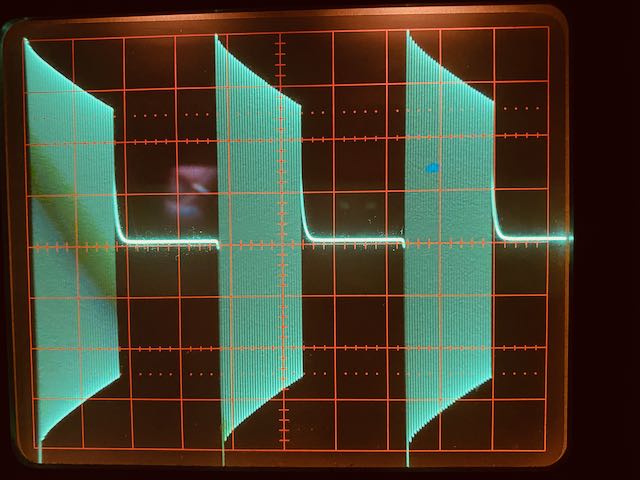
Hier wurde ein Tastverhältnis von 1:1 gewählt, aber obwohl die Schwingungen zu früh abgeschnitten werden, sieht man bereits, wie die Schwingungen langsam abklingen.

Besser ist das mit einem größeren Tastverhältnis zu sehen, wie etwa hier:

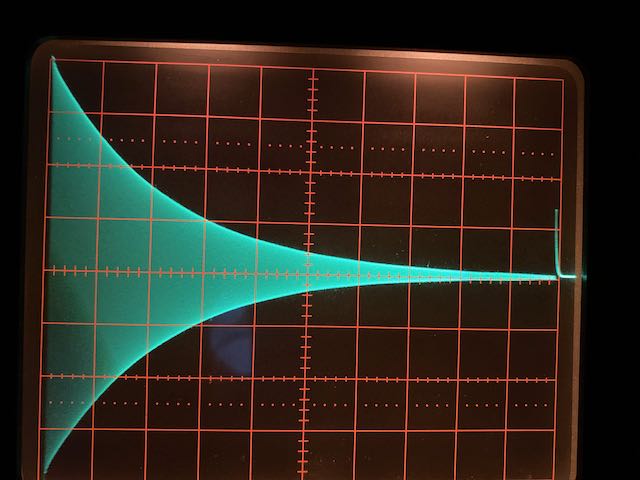
Man erkennt, wie die Amplitude (die Hüllkurve) mit einer e-Funktion abnimmt, denn in jeder Schwingung (die hier nicht mehr aufgelöst werden) verliert der Schwingkreis den gleichen Prozentsatz an Energie (was die Defintion einer e-Funktion ist).

Bei weiterem Hineinzoomen erkennt man die einzelnen Schwingungen des Schwingkreises, verliert jedoch den größeren Überblick:

Dies lässt sich symbolisch wie folgt zusammenfassen:

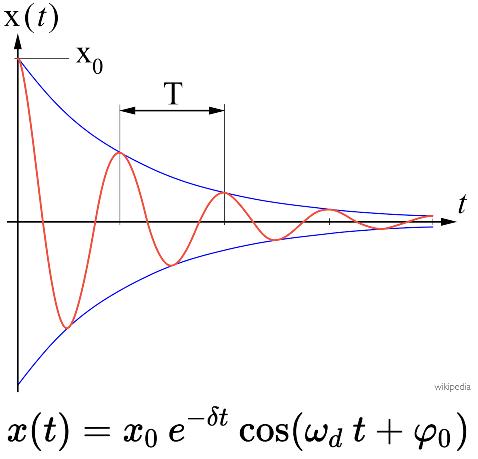
Kommen wir nun endlich zur Güte Q. Sie ist ein Maß für die Dämpfung, wobei eine hohe Güte eine geringe Dämpfung bedeutet. Q ist definiert als das Verhältnis der gespeicherten Energie W zu Beginn einer Periode zum Energieverlust V in dieser Periode, multipliziert mit 2.

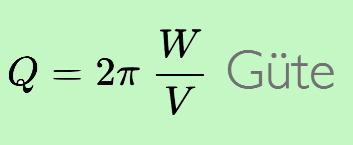
W = 1/2 * C * U² + 1/2 * L * I²

Da wir mit dem Oszi die Spannung U am Kondensator messen und wir für die Hüllkurve nur die Maximalwerte, zu denen alle Energie im Kondensator steckt und der Strom I daher Null ist, betrachten, können wir den zweiten Summanden auch weglassen.

Sei W(0) = 1/2 * C * U₀²  die Startenergie und W(1) = 1/2 * C * U₁² die Energie nach einer Schwingung, so erhalten wir für

V = W(0) - W(1) = 1/2 * C * (U₀² - U₁²)
U₁ = U₀ * exp(- * T)

wobei die Abklingkonstante und T die Periodendauer ist.

T = 1/f, wobei f die Resonanzfrequenz ist

= 2 * f  ====> f = / 2

T = 2 /

U₁ = U₀ * exp(- * 2 / )

Q = 2 * W/V
= 2 * 1/2 C  * U₀² / (1/2 C  (U₀² - U₁²))
= 2 * U₀² / (U₀² - U₁²)       ; Einsetzen von U₁
= 2 * U₀² / (U₀² * ( 1 - exp( - 2 * 2  / ) ) )     ; die erste 2 kommt vom Quadrieren!
= 2 / ( 1 - exp(- 4   D) )           ; D =   /              ; Näherung exp(x) = 1 + x
= 2 / ( 1 - 1 - ( -4 D)
= 2 /  4 D
= 1 / (2 D)

Q messen
Wie können wir aber nun die Güte messen? Dafür gibt es verschiedene Möglichkeiten.

1) Wir betrachten die Hüllkurve und bestimmen die Zeit, bis die Amplitude auf einen bestimmten Wert abgesunken ist. Für die Hüllkurve gilt ja:

U(t) = U₀ * exp(- * t)

Legen wir nun fest, dass wir die Zeit messen, bis die Hüllkurve auf den Wert  exp(-1) = 1 / e = 0.37 der Ausgangsamplitude U₀ abgesunken ist, so bekommen wir Q recht einfach:
wir bestimmen so am Oszi, dass

U(t) = U₀ / exp(1) = U₀ / 2.718 = U₀ * 0.37

U₀ / exp(1) = U₀ * exp(- * )
exp(-1) = exp(- * )             ; Vergleich der Exponenten
-1 = - *
= 1 /

Wenn wir nun in die obige Formel für Q einsetzen, so erhalten wir

Q = / (2 ) = (   * ) / 2

Q =  (   * ) / 2 = * f *

2) Verwenden wir nun die Periodendauer T = 2 /   so erhalten wir

Q =  (   * ) / 2 =  ( 2 / T  * ) / 2 = * / T

Q = * / T

Das Verhältnis / T gibt aber gerade an, wieviele Perioden bis zum Absinken auf  den 1/e-ten Wert vollendet wurden. Wir können also am Oszi einfach abzählen, wieviele Perioden reinpassen, bis die Spannung auf 1 / e der Startspannung abgesunken ist. Dies ist aber nur praktikabel, wenn die Güte nicht zu hoch ist, sonst verzählt man sich dabei sicher!

Man kann auch einfach n Schwingungen abzählen und die Spannungen U₀ und U_n messen. Es gilt dann

Q = (n * ) / ln(U₀ / U_n)

3) Durch Messung der Resonanzüberhöhung der Spannung am Schwingkreis (dies verwendet das QM-1 Q-Meter von Heathkit, siehe meine andere Seite).

4) Durch Messung der Bauteilgüte (eher nicht wirklich)

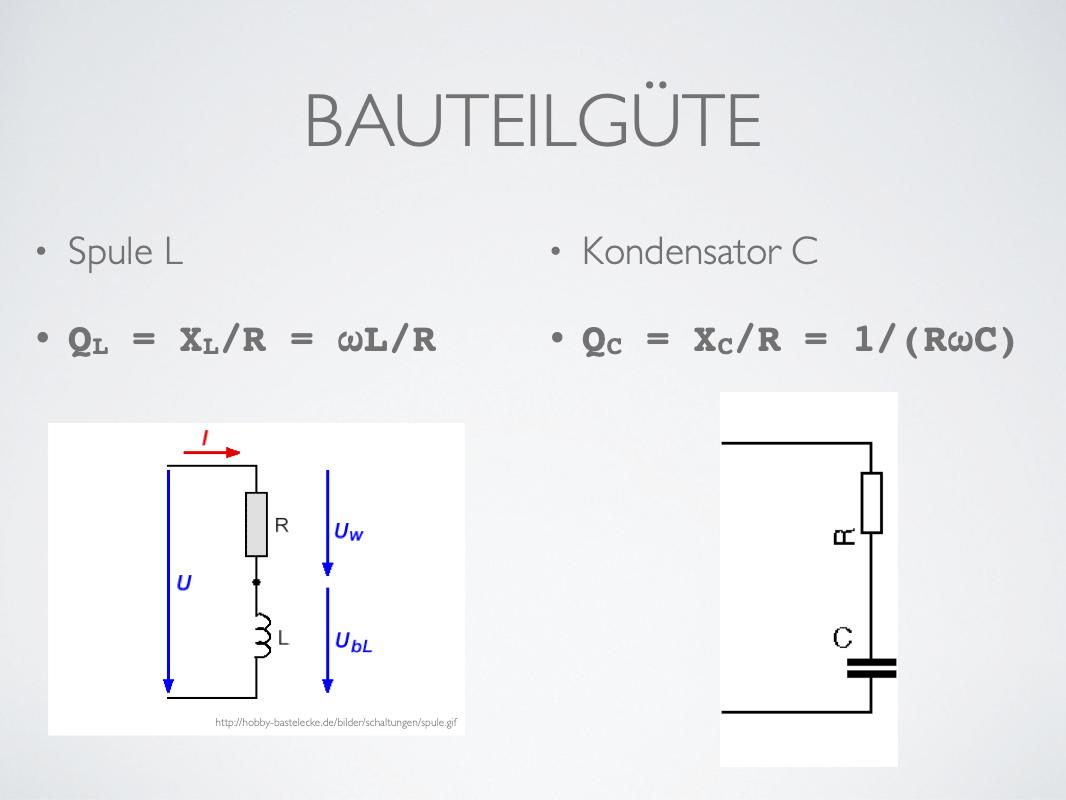
Wie wähle ich L und C?

Methodenvergleich
Wir vergleichen nun die gemessenen Q-Werte nach der Hüllkurvenmethode und der Resonanzmethode (QM-1). Dazu verwende ich eine Spule aus HF-Litze, gewickelt über zwei Ferritstäbe. Die Spule ist am QM-1 angeschlossen, aber mit einem grossen Parallelkondensator von  C =16,88 nF + 1,398 nF = 18,278 nF auf eine Resonanzfrequenz f = 20 kHz. Bei Benutzung des Oszi wird der 5 nF Padding-Kondensator im QM-1 kurzgeschlossen, weil sonst aufgrund der Masseverhältnisse eine sehr grosse Brummspannung eingekoppelt wird. Daher ist die Resonanzfrequenz mit dem Oszi etwas niedriger als mit dem QM-1.

Aus der Schwingkreisformel können wir mit f = 20 kHz und C = 18,278 nF die Induktivität L der Spule berechnen

L = 1 / (2 * * f)² * C = 3,46 mH

Durch Auszählen der Kästchen sinkt die Amplitude auf den 1/e-ten Teil wenn sie von 4 Kästchen auf 4/e = 1,5 Kästchen gefallen ist.

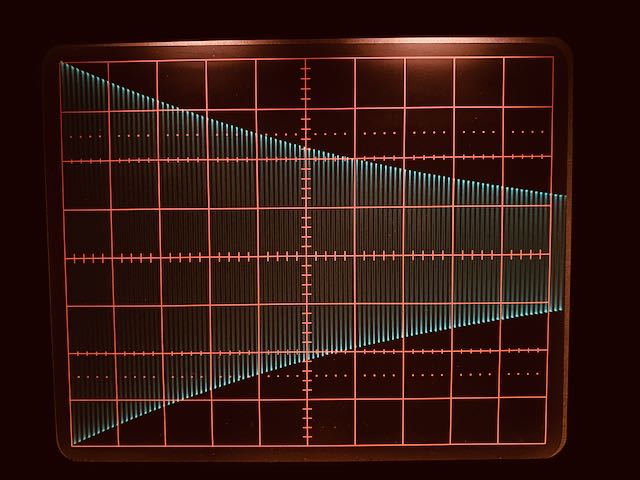
Bei 0,5 ms pro Kästchen ist dies nach 9 Kästchen der Fall. Also = 4,5 ms. Die Periodendauer T = 1 / f = 1 / 20 kHz = 50 s. Somit ist die Güte

Q  = * / T = * 4,5 ms / 50 s = * 90 = 283

Nun zur Bestimmung mit dem QM-1.  Es wird der gleiche Parallel-Schwingkreis-Kondensator C =16,88 nF + 1,398 nF = 18,278 nF verwendet, jedoch bleibt der Padding-Kondensator von 5,000 nF + 16,88 nF = 21,88 nF in der Schaltung. Die effektive Schwingkreis-Kapazität verringert sich also auf  1 /18,278 nF + 1 / 21,88 nF = 1 / C, C = 9,96 nF und damit steigt die Resonanzfrequenz auf f = 27,62 kHz. Die Eichung erfolgt auf den "X1" Punkt. Abgelesen wird ein Q = 70. Aufgrund des größeren Padding-Kondensators von 21,88 nF liegt nun aber eine um den Faktor  5,00 nF / 21,88 nF = 0,229 kleinere Spannung als bei der Kalibration an, daher muss das abgelesene Q mit dem Kehrwert dieses Faktors multipliziert werden, da es ja tatsächlich höher ist. Somit ergibt sich Q zu

Q = 70 / 0,229 = 306

Die beiden Werte weichen nur um 7,6 % voneinander ab, was angesichts der vielen ungenauen Ablesungen eine sehr gute Übereinstimmung ist.

Aus der Schwingkreisformel können wir mit f = 27,62 kHz und C = 9,96 nF die Induktivität L der Spule berechnen

L = 1 / (2 * * f)² * C = 3,33 mH

Das ist nur eine Abweichung von ca. 4 % und damit ebenfalls als sehr gut zu bezeichnen, zumal die Frequenzen ja leicht unterschiedlich sind. Ausserdem wurde die unterschiedliche Stellung des Abstimmdrehkos nicht berücksichtigt, da vergessen wurde, diese zu notieren.

Zurück zur Hauptseite